En el ámbito del análisis de datos, comprender las relaciones entre diferentes variables es crucial para tomar decisiones informadas y estratégicas. La Correlación de Pearson, también conocida como coeficiente de correlación lineal de Pearson, es una herramienta estadística ampliamente utilizada para medir la fuerza y la dirección de la relación lineal entre dos variables cuantitativas. Esta técnica no solo es esencial para investigadores y científicos, sino también para profesionales de negocios que buscan optimizar procesos y estrategias basadas en datos. En este artículo, exploraremos la importancia de la Correlación de Pearson, su aplicación práctica y cómo puede mejorar la precisión y la efectividad de tus análisis.
¿Qué es la correlación de Pearson?
La correlación de Pearson es una herramienta estadística utilizada para cuantificar la fuerza y la dirección de la relación lineal entre dos variables continuas. En otras palabras, indica cómo cambia una variable cuando la otra variable cambia de acuerdo a una relación lineal.
El coeficiente de correlación de Pearson, representado por 𝑟, tiene un rango de valores entre -1 y 1. Un valor de 1 indica una correlación positiva perfecta, lo que significa que las dos variables aumentan juntas en una relación lineal perfecta. Un valor de -1 indica una correlación negativa perfecta, lo que significa que una variable aumenta mientras la otra disminuye en una relación lineal perfecta. Un coeficiente de correlación de Pearson de 0 indica que no existe una relación lineal aparente entre las dos variables.
La fórmula para el coeficiente de correlación de Pearson es:
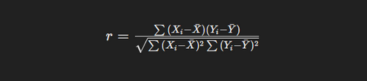
Donde:

La correlación de Pearson es ampliamente utilizada en diversos campos, como la economía, la psicología, la biología, la investigación de mercados y muchas otras disciplinas, para analizar y comprender la relación entre diferentes variables. Sin embargo, es importante tener en cuenta que la correlación de Pearson solo mide la relación lineal y puede no capturar relaciones no lineales entre variables. En tales casos, otras medidas de correlación, como la correlación de Spearman o la correlación de Kendall, pueden ser más apropiadas.
Importancia de la correlación de Pearson
La importancia de la correlación de Pearson radica en su capacidad para cuantificar y evaluar la relación lineal entre dos variables continuas. Algunas de las razones clave por las cuales la correlación de Pearson es importante incluyen:
Medición de la relación: Proporciona una medida cuantitativa de la fuerza y la dirección de la relación entre dos variables. Esto permite a los investigadores, incluidos aquellos en análisis de datos e investigación de mercados, comprender mejor cómo cambia una variable cuando la otra variable cambia en una relación lineal.
Identificación de patrones: Ayuda a identificar patrones y tendencias en los datos, lo que es esencial en el análisis de datos para descubrir insights significativos. Si dos variables están altamente correlacionadas, puede sugerir que están relacionadas de alguna manera y pueden influirse entre sí, lo cual es fundamental en la investigación de mercados para comprender el comportamiento del consumidor.
Validación de teorías y modelos: Permite validar teorías y modelos propuestos en diversas disciplinas. Por ejemplo, en la economía, la correlación entre el precio de un producto y la demanda puede validar la teoría de la ley de la oferta y la demanda.
Predicción y toma de decisiones: La correlación de Pearson se utiliza en la predicción de variables, lo cual es crucial en el análisis de datos y la investigación de mercados para tomar decisiones informadas. Si dos variables están fuertemente correlacionadas, se puede usar una para predecir la otra con mayor precisión.
Control de calidad y mejora de procesos: En campos como la ingeniería y la fabricación, la correlación de Pearson se utiliza para evaluar la relación entre variables de proceso y parámetros de calidad, lo que es esencial para mejorar los procesos y garantizar la calidad de los productos.
Investigación científica: En disciplinas como la psicología, la biología y la sociología, la correlación de Pearson se utiliza para investigar las relaciones entre variables y para comprender mejor los fenómenos complejos que se estudian en estas áreas.
En conclusión, la correlación de Pearson es una herramienta estadística poderosa y ampliamente utilizada que proporciona información crucial para la comprensión, predicción y toma de decisiones en una variedad de campos y disciplinas.
Aplicaciones de la correlación de Pearson en el análisis de datos
La correlación de Pearson tiene numerosas aplicaciones en el análisis de datos. Aquí se presentan algunas de las más destacadas e importantes:
- Identificación de relaciones lineales: La correlación de Pearson es útil para identificar relaciones lineales entre variables. Esto es fundamental en el investigación exploratoria de datos para comprender cómo las variables están relacionadas entre sí.
- Selección de características: En el análisis de datos y aprendizaje automático, la correlación de Pearson puede ayudar en la selección de características. Se pueden identificar las variables que están altamente correlacionadas con la variable objetivo, lo que puede ayudar a reducir la dimensionalidad y mejorar la precisión del modelo.

- Validación de hipótesis: La correlación de Pearson se utiliza para las pruebas de hipótesis sobre relaciones entre variables. Por ejemplo, en estudios científicos, puede ayudar a respaldar o refutar teorías propuestas.
- Análisis de tendencias: La correlación de Pearson puede ayudar a identificar tendencias en los datos. Por ejemplo, en el análisis financiero, se puede utilizar para evaluar la relación entre variables como el precio de las acciones y los ingresos de una empresa a lo largo del tiempo.
- Predicción y modelado: La correlación de Pearson se utiliza en la construcción de modelos predictivos. Si dos variables están altamente correlacionadas, una puede usarse para predecir la otra con mayor precisión.
- Análisis de mercado: En investigación de mercados, la correlación de Pearson puede utilizarse para comprender la relación entre variables como el precio de un producto y la demanda, o la percepción de calidad y la satisfacción del cliente.
- Análisis de relaciones: La correlación de Pearson puede ayudar a entender cómo se relacionan entre sí diferentes variables en un conjunto de datos. Por ejemplo, en estudios sociales, puede utilizarse para examinar la relación entre variables como la educación y los ingresos.
La correlación de Pearson es una herramienta poderosa en el análisis de datos que se utiliza para identificar relaciones, validar hipótesis, realizar predicciones y comprender mejor los datos en una amplia gama de campos y aplicaciones. Su capacidad para cuantificar la relación lineal entre variables continuas la convierte en una herramienta invaluable en la exploración y comprensión de conjuntos de datos complejos.
Conclusión
La correlación de Pearson es, sin duda, una herramienta invaluable en el vasto mundo del análisis de datos. Su capacidad para identificar y medir relaciones lineales entre variables es fundamental para desentrañar los secretos ocultos en conjuntos de datos complejos. Al aplicar correctamente la Correlación de Pearson, se pueden obtener insights significativos que pueden impulsar la toma de decisiones informadas en una amplia variedad de campos y disciplinas.
En Berumen, nuestra agencia de investigación de mercados, comprendemos la importancia de esta herramienta y estamos aquí para ayudarte a aprovechar al máximo su potencial. Ya sea que estés buscando comprender mejor el comportamiento del consumidor, validar hipótesis en tu empresa o mejorar tus estrategias de marketing, podemos brindarte la asesoría y el apoyo necesarios.
Ponte en contacto con nosotros ahora mismo y descubre cómo podemos trabajar juntos para implementar y utilizar la correlación de Pearson en tus análisis de datos. En Berumen, estamos comprometidos a ayudarte a alcanzar tus objetivos y a desbloquear el máximo valor de tus datos. ¡No dudes en contactarnos y comenzar a dar forma a tu éxito hoy mismo!



